Đề thi thử vào Lớp 10 môn Toán - Năm học 2019-2020 - Trường THCS Châu Can (Có đáp án)

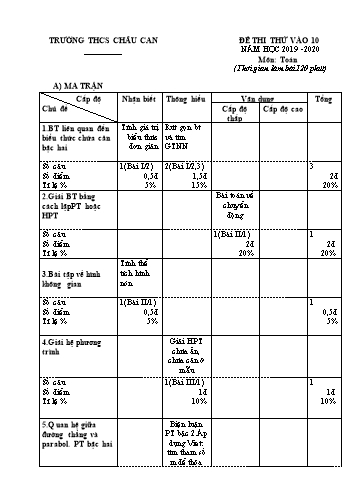
 TRƯỜNG THCS CHÂU CAN ĐỀ THI THỬ VÀO 10
 NĂM HỌC 2019 -2020
 Môn: Toán 
 (Thời gian làm bài 120 phút)
 A) MA TRẬN
 Cấp độ Nhận biết Thông hiểu Vận dụng Tổng
Chủ đề Cấp độ Cấp độ cao
 thấp 
1.BT liên quan đến Tính giá trị Rút gọn bt 
biểu thức chứa căn biểu thức và tìm 
bậc hai đơn giản GTNN
Số câu 1(Bài I/2) 2(Bài I/2,3) 3
Số điểm 0,5đ 1,5đ 2đ
Tỉ lệ % 5% 15% 20%
2.Giải BT bằng Bài toán về 
cách lậpPT hoặc chuyển 
HPT động
Số câu 1(Bài II/1) 1
Số điểm 2đ 2đ
Tỉ lệ % 20% 20%
 Tính thể 
3.Bài tập về hình tích hình 
không gian nón
Số câu 1(Bài II/1) 1
Số điểm 0,5đ 0,5đ
Tỉ lệ % 5% 5%
4.Giải hệ phương Giải HPT 
trình chứa ẩn, 
 chứa căn ở 
 mẫu
Số câu 1(Bài III/1) 1
Số điểm 1đ 1đ
Tỉ lệ % 10% 10%
5.Quan hệ giữa Biện luận 
đường thẳng và PT bậc 2.Áp 
parabol. PT bậc hai dụng Viet: 
 tìm tham số 
 m để thỏa B)ĐỀ BÀI
Bài I: (2,0đ)
 x 15 2 x 5 x 1
Cho hai biểu thức : M ; N : x 0; x 1; x 9 
 x 3 x 3 x 9 x 3
1) Tính giá trị của M khi x=81
2) Rút gọn biểu thức N
3) Tìm giá trị nhỏ nhất của biểu thức: P=M+N 
Bài II (2,5đ) 
1)Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
 Một ôtô khách và một ôtô tải cùng xuất phát từ địa điểm A đi đến địa điểm B 
đường dài 180 km do vận tốc của ôtô khách lớn hơn ôtô tải 10 km/h nên ôtô khách 
đến B trước ôtô tải 36 phút.Tính vận tốc của mỗi ôtô. Biết rằng trong quá trình đi 
từ A đến B vận tốc của mỗi ôtô không đổi.
2) Một chiếc ly đựng nước có dạng hình nón với chiều cao 12,5cm và có diện tích 
đáy là 28,26cm2. Hỏi chiếc ly đó đựng đầy được bao nhiêu cm3 nước? ( Bỏ qua bề 
dày của ly nước).
Bài III(2,0đ)
 1 1
 3
 x 1 y 2
1. Giải hệ phương trình: 
 3 2
 1
 x 1 y 2
2. Cho các hàm số :
 y = x2 (P) và y = 3x + m2 (d)
 ( x là biến số , m là tham số cho trước)
a) Chứng minh rằng với bất kỳ giá trị nào của m, đường thẳng (d) luôn cắt 
parabol(P) tại 2 điểm phân biệt.
b) Gọi y1 và y2 là tung độ các giao điểm của đường thẳng (d) và parabol(P).Tìm m 
để có đẳng thức : y1 + y2 = 11y1.y2 
Bài IV: (3,0đ)Cho đường tròn tâm O, đường kính AB cố định.Điểm H thuộc đoạn 
thẳng OA (H khác O,A và H không là trung điểm của OA).Kẻ MN vuông góc với 
AB tại H.Gọi K là điểm bất kỳ của cung lớn MN(K khác M,N và B).Các đoạn 
thẳng AK và MN cắt nhau tại E.
 1/Chứng minh bốn điểm H,E,K,B nội tiếp được trong một đường tròn
 2/Chứng minh tam giác AME đồng dạng với tam giác AKM
 3/Cho điểm H cố định, xác định vị trí điểm K sao cho khoảng cách từ N 
đến tâm đường tròn ngoại tiếp tam giác KME nhỏ nhất.
Bài V(0,5đ): 
Cho các số thực a, b, c thỏa mãn điều kiện 0 £ a,b,c £ 2 và a + b + c = 3
 a2 + b2 + c2
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức. P =
 ab + bc + ca Vậy vận tốc của xe khách là 60(km/h) 0,25
 Vận tốc xe tải là: 60 - 10 = 50(km/h)
 1 1
 2)Thể tích chiếc ly hình nón là: V S.h .28,26.12 113,04(cm3 )
 3 3 0,5
 Hay 113,04ml
 1.Điều kiện x>1và y 2 . Đặt
 1
 a 
 x 1
 1
 b 
 y 2
 với a>0 và b 0
 Ta có HPT 
 0,5đ
 a b 3
 Giải HPT ta được a=1(TMĐK) và b=-2 (TMĐK)
 3a 2b 1
 Từ đó tìm được x=2 và y= 5 (TMĐK) 0,25đ
 2
 5
 Vậy hệ phương trình có nghiệm duy nhất là ( x, y ) = ( 2 ; ). 0,25đ
 2
 2) 
 a) Hoành độ giao điểm của parabol (P) và đường thẳng (d) là nghiệm của 
 phương trình : x2 = 3x + m2
Bài 
 x2 - 3x - m2 = 0 (*) 
III 
 Phương trình (*) có : = 9 + 4m2 > 0 với mọi m 
(2đ) 0,5đ
 => phương trình (*) luôn có hai nghiệm phân biệt với mọi m 
 => Đường thẳng (d) bao giờ cũng cắt parabol (P) tại hai điểm phân biệt 
 với mọi m 
 b)Gọi A và B là giao điểm của đường thẳng (d) và para bol (P) và toạ độ 
 giao điểm của chúng là: 
 A(x1; y1) ; B(x2 ; y2)
 Áp dụng hệ thức viet cho phương trình (*) ta có :
 x1 x2 3
 2 
 x1.x2 m
 2 2 2
 Ta có y1 + y2 = ( 3x1 + m ) + (3x2 + m ) = 3(x1 + x2) + 2m 
 = 2m2 + 9 (1)
 2 2 2 2 2 4
 và y1.y2 = x1 .x2 = (x1.x2) = (-m ) = m (2)
 Từ (1) và (2) ta có :
 y1 + y2 = 11y1 .y2
 2m2 + 9 = 11 m4 (3) 0,25đ
 11m4 – 2m2 – 9 = 0 Xét AME và AKM có :
 M· AK chung 0,5đ
 A· KM A· ME AME : AKM (g.g) 
 3) Gọi O' là tâm đường tròn ngoại tiếp tam giác KME.
 Ta có ·AME ·ABM nên ta chứng minh được AM là tiếp tuyến của đường 0,5đ
 tròn (O') tại M.
 Từ đó suy ra O' thuộc MB. 0,25đ
 Vậy khoảng cách từ N đến O' nhỏ nhất khi NO' vuông góc với MB.
 Từ đó tìm được vị trí điểm K: Từ N kẻ NO' vuông góc với MB. 
 Vẽ (O', O'M) cắt đường tròn tâm O tại K. 0,25đ
 • Tìm Min
 Do (a- b)2 +(b- c)2 +(c- a)2 ³ 0 với mọi a, b, c suy ra 
 a 2 + b2 + c2 ³ ab + bc + ca
 Từ đó ta có:
 a2 + b2 + c2 ab + bc + ca
 P = ³ = 1 0,25đ
 ab + bc + ca ab + bc + ca
Bài V Dấu đẳng thức xảy ra khi và chỉ khi a = b = c = 1
(0,5đ) Vậy minP = 1.
 • Tìm Max
 Do 0 £ a,b,c £ 2 nên (a - 2)(b - 2)(c - 2)£ 0
 Û abc - 2(ab + bc + ca)+ 4(a + b + c) - 8 £ 0
 Û 2(ab + bc + ca)³ 4+ abc ³ 4
 ab bc ca 2
 a2 + b2 + c2 9 9 5
 Từ đó, P = = - 2 £ - 2 = 0,25đ
 ab + bc + ca ab + bc + ca 2 2
 Dấu đẳng thức xảy ra khi và chỉ khi a = 2,b = 1,c = 0 và các hoán vị của 
 chúng
 5
 Vậy max P =
 2
 Duyệt của BGH